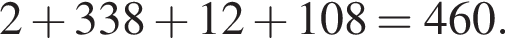На изготовление 25 письменных столов расходуется 3,4 м3 древесины. Сколько кубических метров древесины потребуется на изготовление 110 таких столов?
Функция 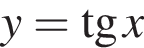 не определена в точке:
не определена в точке:
Если 15% некоторого числа равны 33, то 20% этого числа равны:
График уравнения 1,8x − 0,6y = a проходит через точку А(−2; 9). Найдите число a.
Укажите номер выражения, которое определяет, сколько сантиметров в х м 9 дм.
| 1) 100х + 9; | 2) 100х + 90 | 3) 90x | 4) 10x + 90 | 5) 10x + 9 |
Среди чисел ![]()
![]()
![]()
![]()
![]() укажите то, которое является решением системы неравенств
укажите то, которое является решением системы неравенств 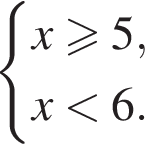
Прямая a, параллельная плоскости α, находится от нее на расстоянии 6. Через прямую a проведена плоскость β, пересекающая плоскость α по прямой b и образующая с ней угол 60°. Найдите площадь четырехугольника ABCD, если A и B — такие точки прямой a, что AB = 4, а C и D — такие точки прямой b, что CD = 3.
Найдите длину средней линии прямоугольной трапеции с острым углом 60°, у которой большая боковая сторона и большее основание равны 10.
На одной стороне прямого угла О отмечены две точки А и В так, что ОА = 1,7, OB = а, ОА < ОВ. Составьте формулу, по которой можно вычислить радиус r окружности, проходящей через точки А, В и касающейся другой стороны угла.
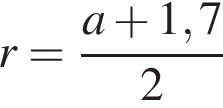
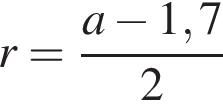
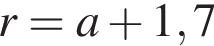
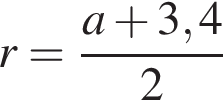
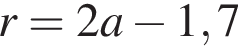
Укажите номера верных неравенств, если известно, что 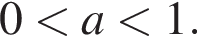

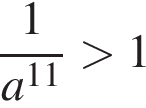
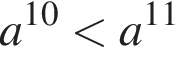
На круговой диаграмме представлена информация о продаже 200 кг овощей в течение дня. Для начала каждого из предложений А — В подберите его окончание 1 — 6 так, чтобы получилось верное утверждение.
А) Масса (в килограммах) проданной капусты равна ...
Б) Отношение, выраженное в процентах, которое показывает, на сколько масса проданного картофеля меньше массы проданных помидоров, равно ...
В) Отношение, выраженное в процентах, которое показывает, на сколько масса проданной свеклы больше массы проданного лука, равно ...
1) 25
2) 40
3) 4
4) 125
5) 38
6) 19
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Выберите три верных утверждения:
1) если 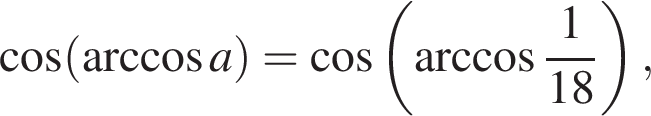 то
то 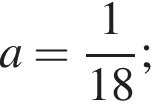
2) если 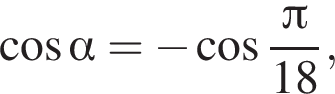 то
то 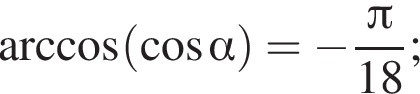
3) если 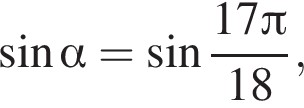 то
то 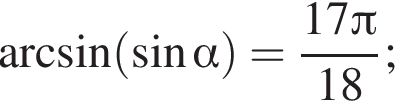
4) если 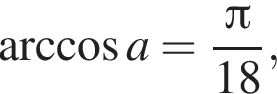 то
то 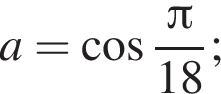
5) если 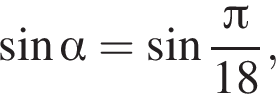 то
то 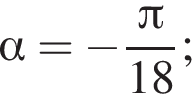
6) если 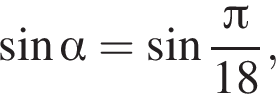 то
то 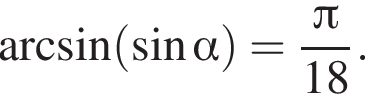
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
Выберите три верных утверждения, если известно, что две перпендикулярные плоскости
![]() и
и ![]() пересекаются по прямой a и точка A принадлежит плоскости
пересекаются по прямой a и точка A принадлежит плоскости ![]() (см. рис.).
(см. рис.).
1. Любая прямая, проходящая через точку A и пересекающая плоскость ![]() пересекает прямую a.
пересекает прямую a.
2. Существует единственная прямая, проходящая через точку A и перпендикулярная плоскости ![]()
3. Прямая, проходящая через точку A и перпендикулярная плоскости ![]() перпендикулярна плоскости
перпендикулярна плоскости ![]()
4. Любая точка прямой a лежит в плоскостях ![]() и
и ![]()
5. Любая прямая, лежащая в плоскости ![]() и перпендикулярная прямой a, перпендикулярна плоскости
и перпендикулярная прямой a, перпендикулярна плоскости ![]()
6. Любая прямая, перпендикулярная прямой a, принадлежит плоскости ![]()
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
На координатной плоскости дана точка A(5; 3). Для начала каждого из предложений А−В подберите его окончание 1–6 так, чтобы получилось верное утверждение.
A) Если точка В симметрична точке А относительно оси ординат, то расстояние между точками А и В равно ...
Б) Если точка С симметрична точке А относительно прямой у = 1, то расстояние между точками А и С равно ...
B) Если точка N симметрична точке А относительно точки D(3; −1), то расстояние между точками А и N равно ...
1) 8
2) 10
3) 4
4) ![]()
5) ![]()
6) ![]()
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Дана геометрическая прогрессия (bn), в которой b5 = 4, b6 = −8. Для начала из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Знаменатель этой прогрессии равен ...
Б) Седьмой член этой прогрессии равен ...
В) Первый член этой прогрессии равен ...
1) ![]()
2) 16
3) −2
4) ![]()
5) −16
6) ![]()
Oтвет запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
В прямоугольном треугольнике ABC
 BH и BK — высота и медиана соответственно, проведенные к гипотенузе (см. рис.). Найдите площадь прямоугольного треугольника ABC, если BK = 7,
BH и BK — высота и медиана соответственно, проведенные к гипотенузе (см. рис.). Найдите площадь прямоугольного треугольника ABC, если BK = 7, 
Найдите значение выражения 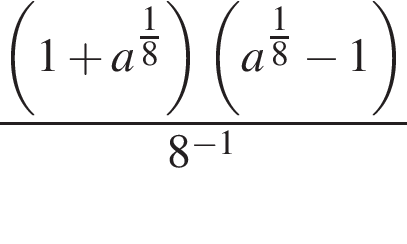 при a = 81.
при a = 81.
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Найдите количество корней уравнения 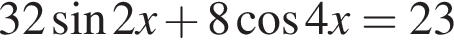 на промежутке
на промежутке 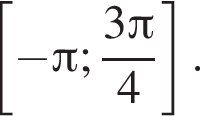
Найдите площадь боковой поверхности правильной треугольной пирамиды, если длина биссектрисы ее основания равна ![]() и плоский угол при вершине
и плоский угол при вершине 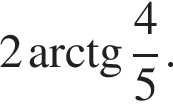
Найдите сумму целых решений неравенства 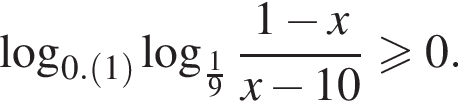
Найдите произведение корней (корень, если он единственный) уравнения 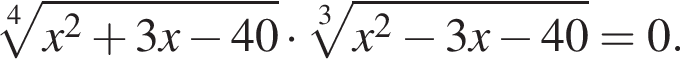
Найдите сумму всех целых решений неравенства 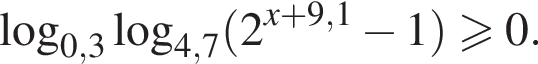
АС — общая гипотенуза прямоугольных треугольников ABC и ADC. Плоскости этих треугольников взаимно перпендикулярны. Найдите квадрат длины отрезка BD, если 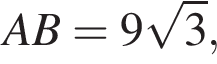
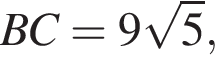 AD = DC.
AD = DC.
Значение выражения 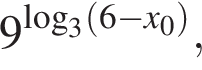 где x0 — корень уравнения
где x0 — корень уравнения 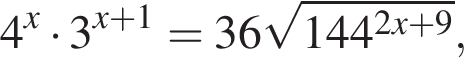 равно ... .
равно ... .
Найдите значение выражения 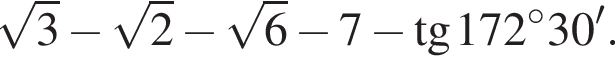
Пусть 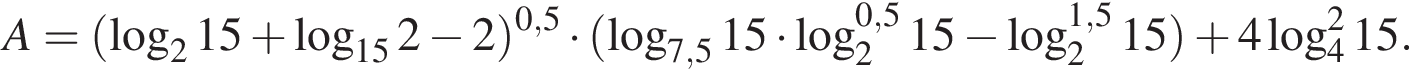
Найдите значение выражения 2A.
Найдите сумму квадратов корней (квадрат корня, если он единственный) уравнения
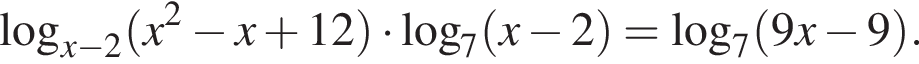
Решите уравнение
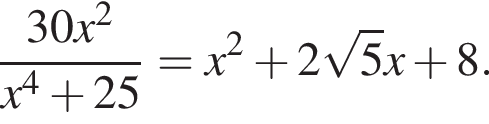
В ответ запишите значение выражения ![]() где x — корень уравнения.
где x — корень уравнения.
Петя записал на доске два различных натуральных числа. Затем он их сложил, перемножил, вычел из большего записанного числа меньшее и разделил большее на меньшее. Сложив четыре полученных результата, Петя получил число 1521. Найдите все такие пары натуральных чисел. В ответ запишите их сумму.

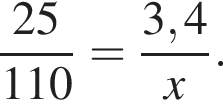 Тогда
Тогда 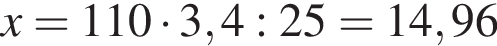 м3.
м3.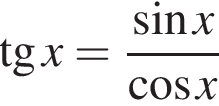 не определена, когда
не определена, когда 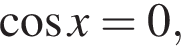 т. е. при
т. е. при 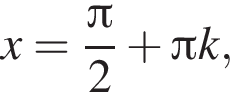 где
где 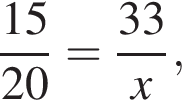 где x — неизвестное число.
где x — неизвестное число.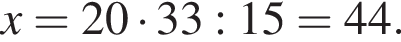
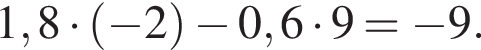

 получаем, что
получаем, что  следовательно, число
следовательно, число 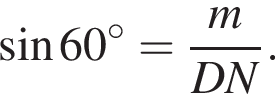
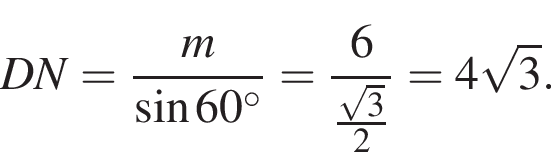
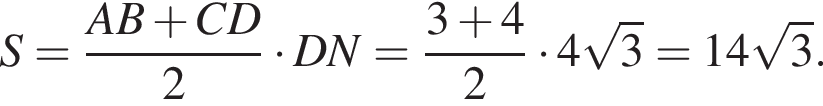
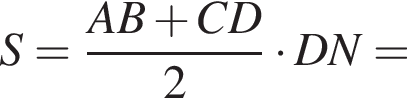
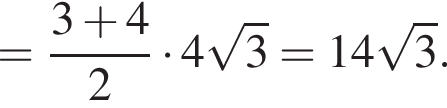
 поэтому
поэтому 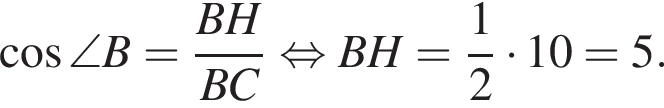 Следовательно,
Следовательно, 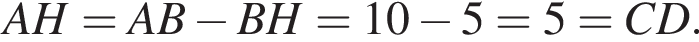
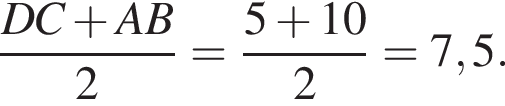
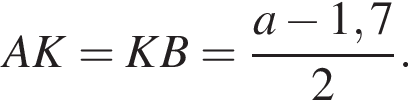
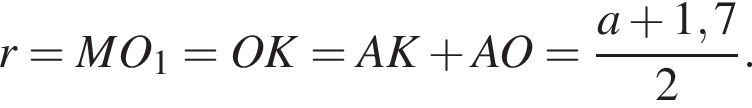
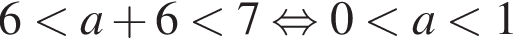 — неравенство верно;
— неравенство верно;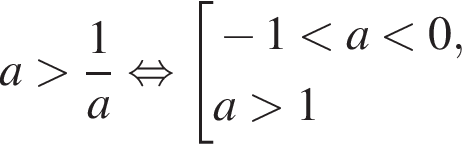 — неравенство неверно;
— неравенство неверно;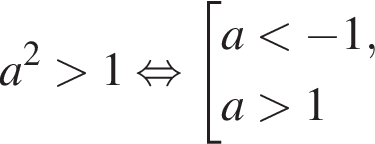 — неравенство неверно;
— неравенство неверно;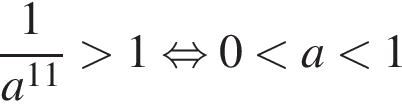 — неравенство верно;
— неравенство верно;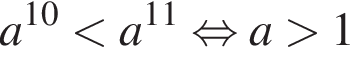 — неравенство неверно.
— неравенство неверно.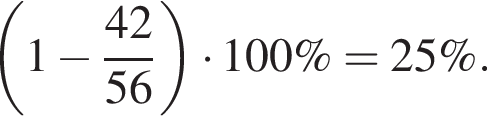
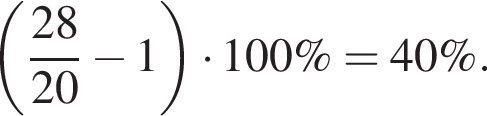
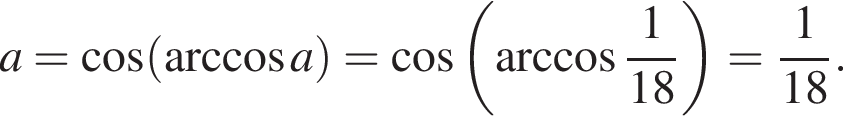

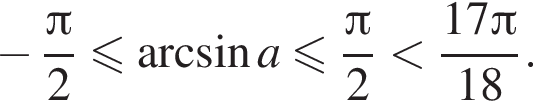
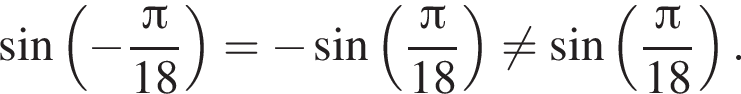
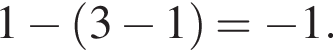 Тогда
Тогда 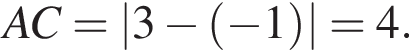
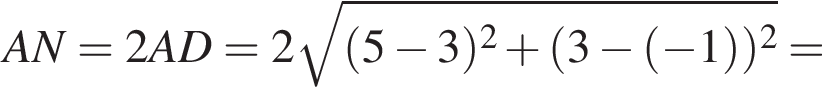
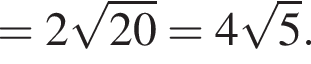
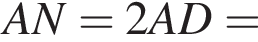
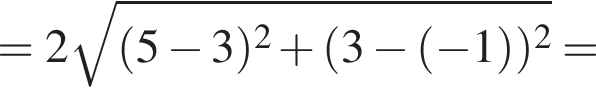
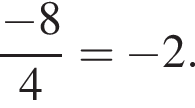
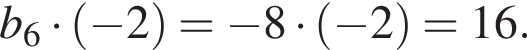
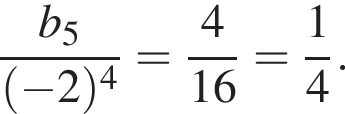
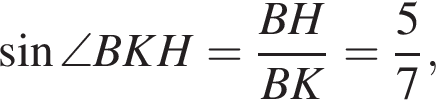 а BK = 7, получаем, что BH = 5. Отрезок BK — медиана прямоугольного треугольника, проведенная к гипотенузе, длина BK равна половине длины гипотенузы, тогда длина гипотенузы равна 2BK = 14. Площадь треугольника ABC равна
а BK = 7, получаем, что BH = 5. Отрезок BK — медиана прямоугольного треугольника, проведенная к гипотенузе, длина BK равна половине длины гипотенузы, тогда длина гипотенузы равна 2BK = 14. Площадь треугольника ABC равна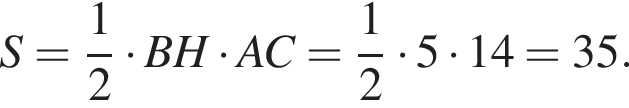
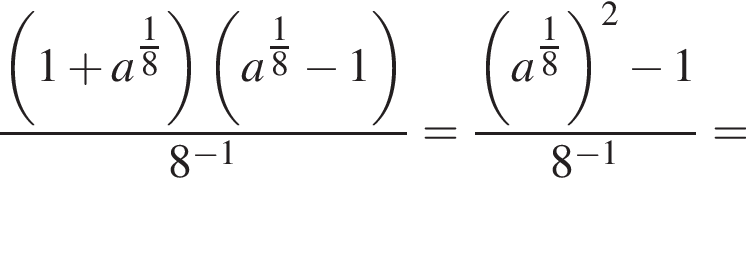
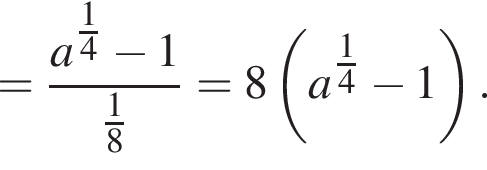
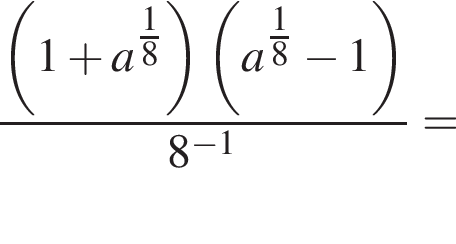
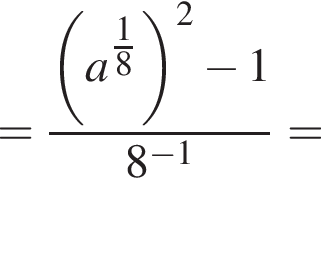
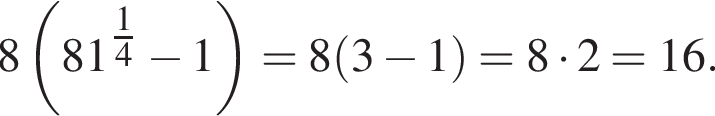
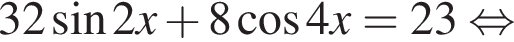
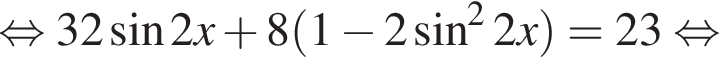
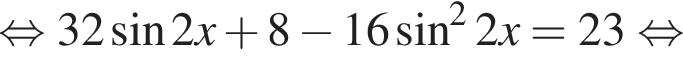
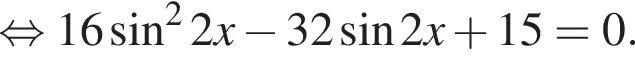
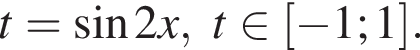 Тогда:
Тогда: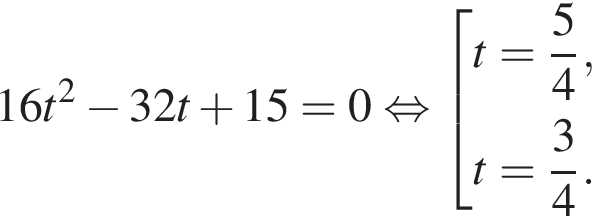
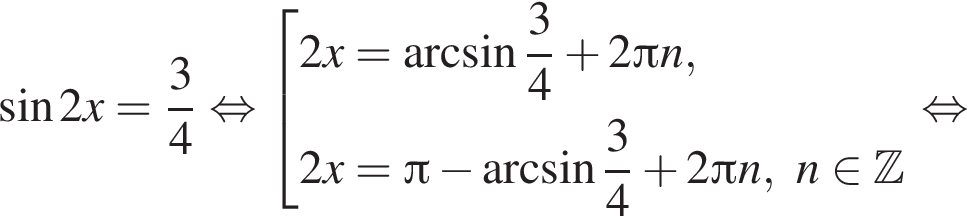
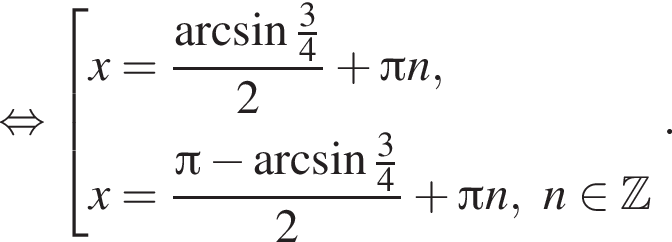
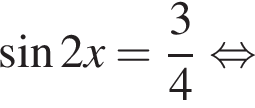
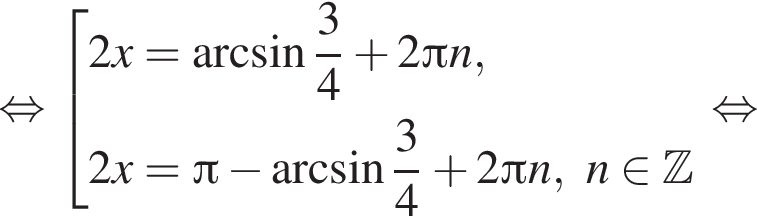
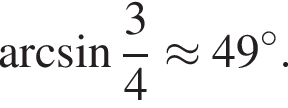 Рассмотрим значения x при различных значениях n:
Рассмотрим значения x при различных значениях n: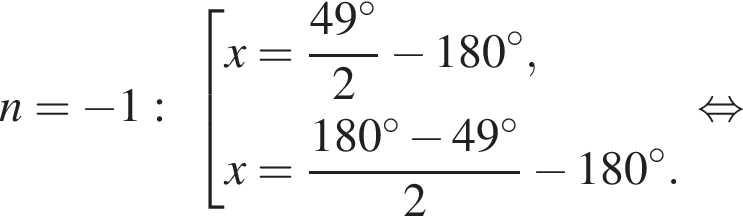
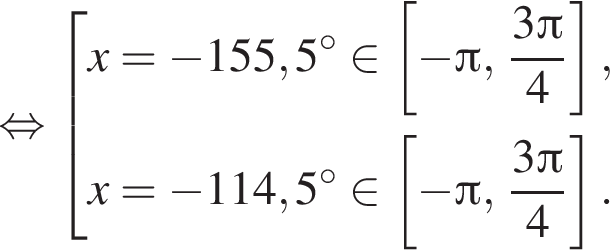
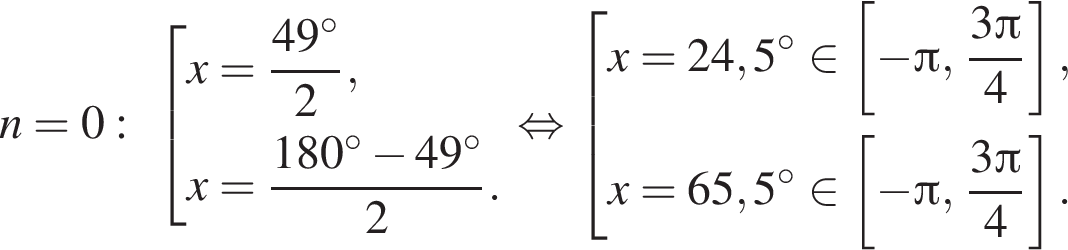
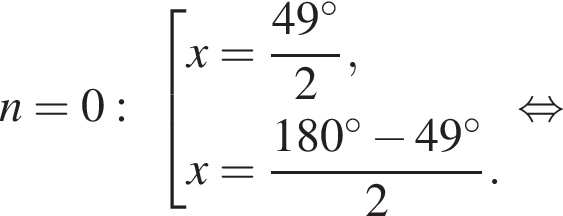
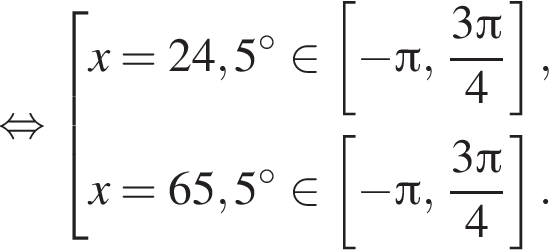

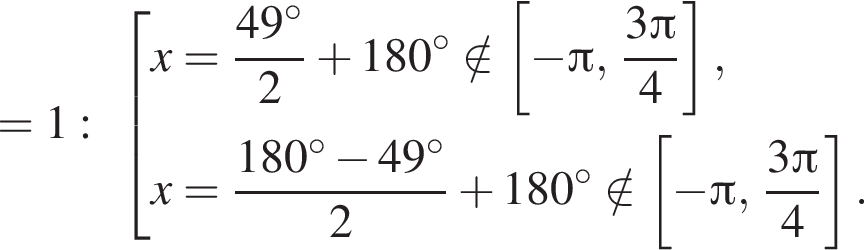
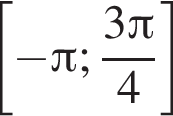 4 корня.
4 корня.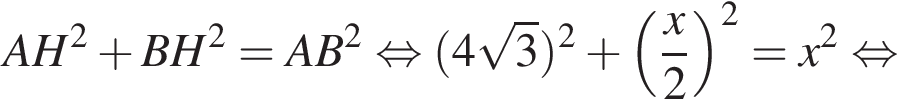
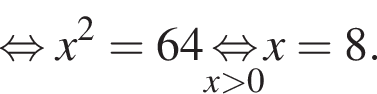
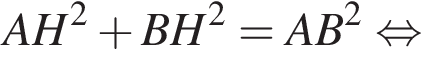
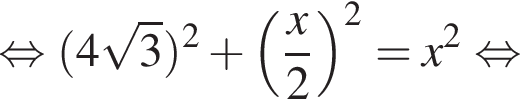
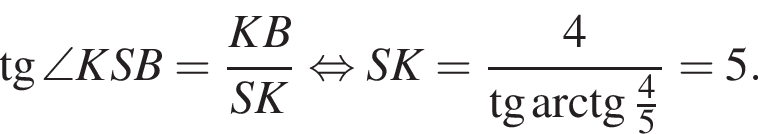 Площадь боковой поверхности равна
Площадь боковой поверхности равна 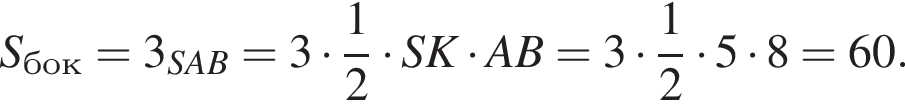
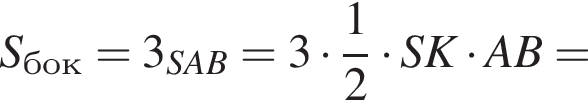
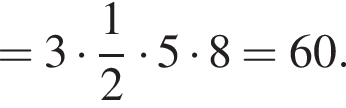
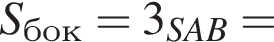
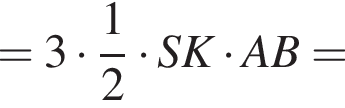
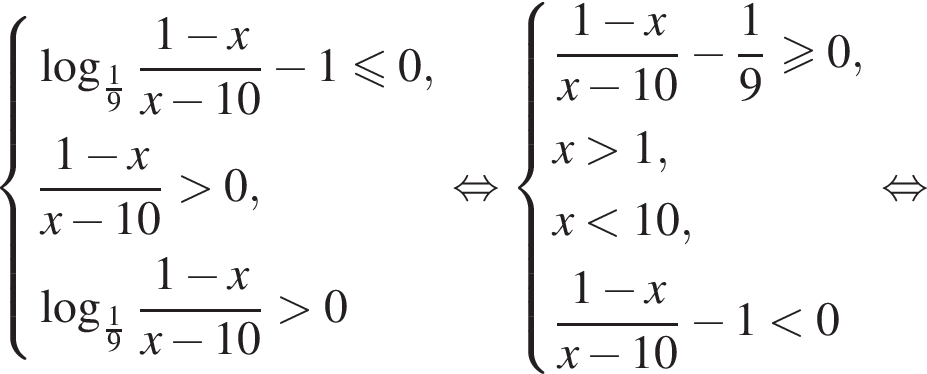
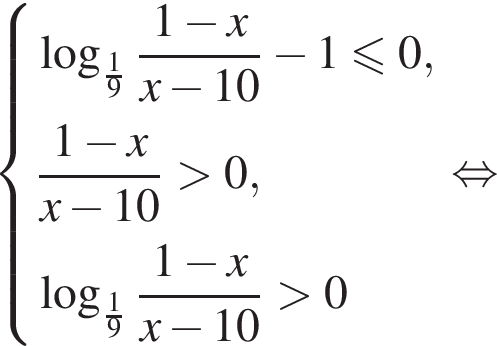
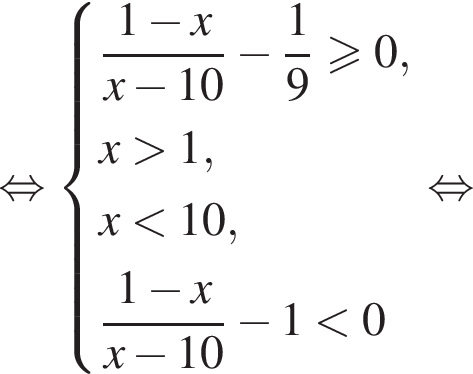
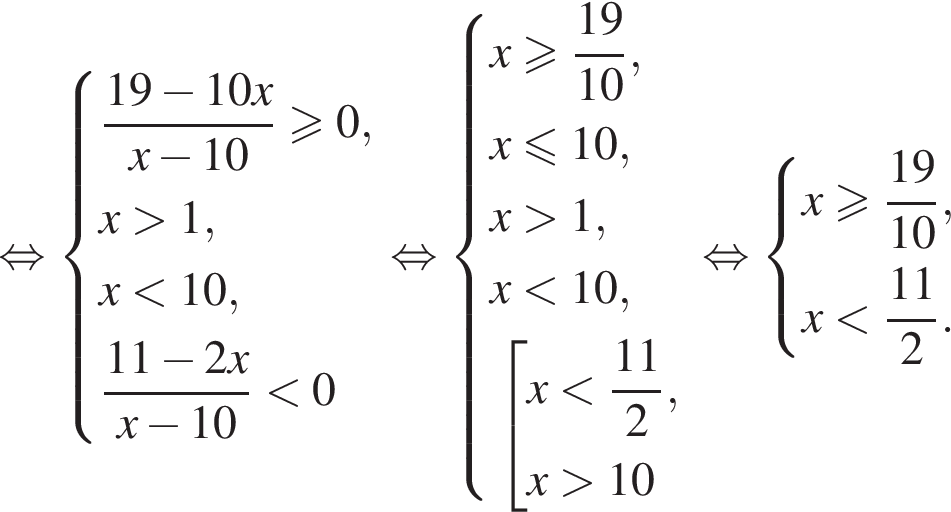
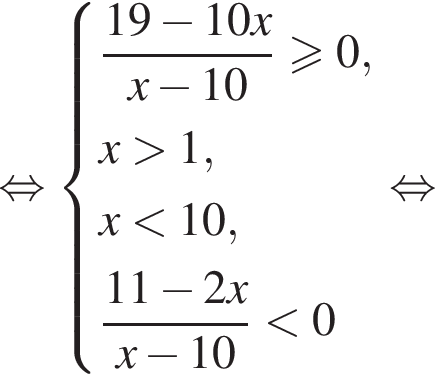
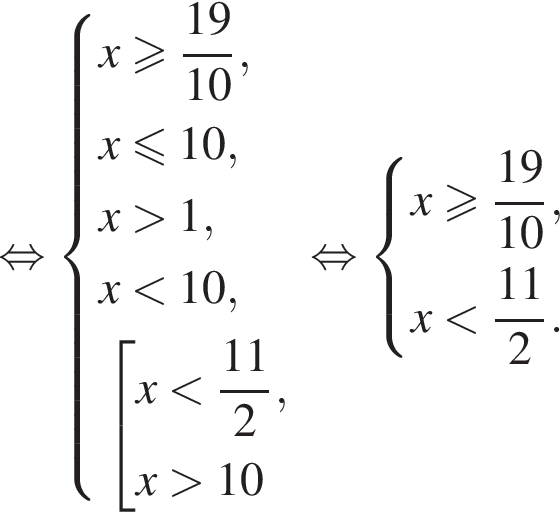
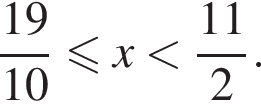 В этот промежуток входят следующие целые числа: 2, 3, 4, 5. Тогда ответом на вопрос задачи будет являться число 14.
В этот промежуток входят следующие целые числа: 2, 3, 4, 5. Тогда ответом на вопрос задачи будет являться число 14.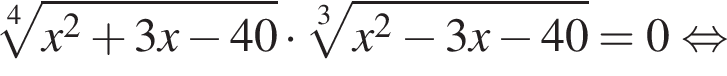
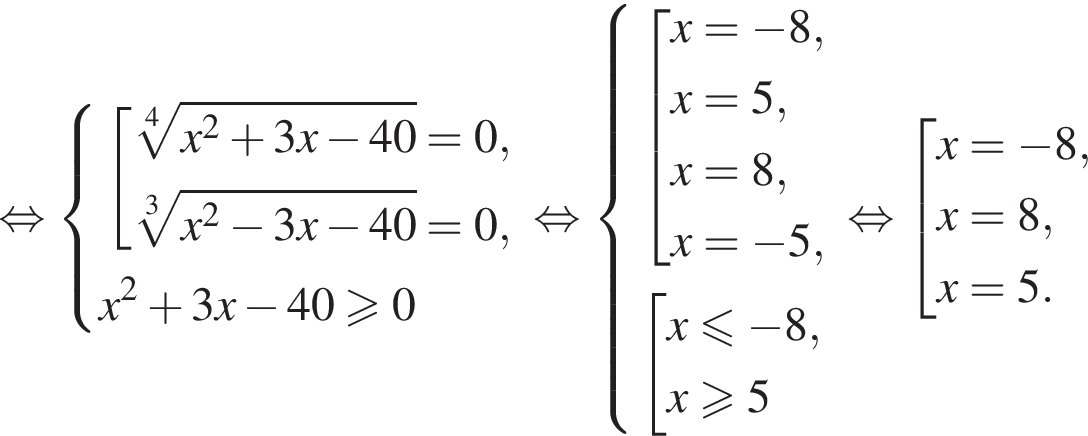
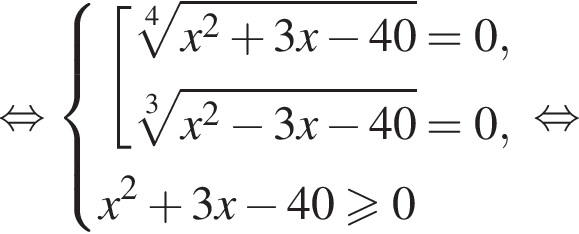
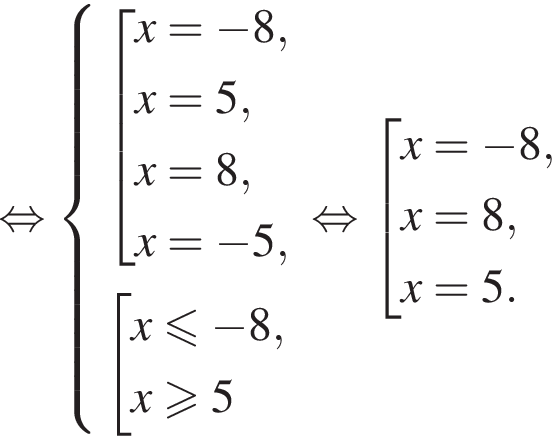
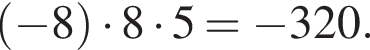
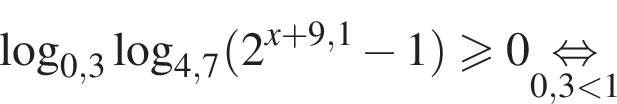
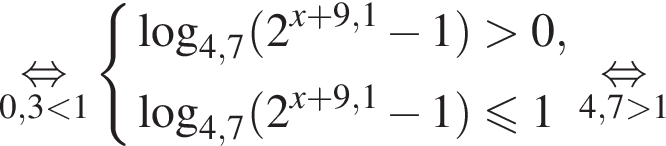
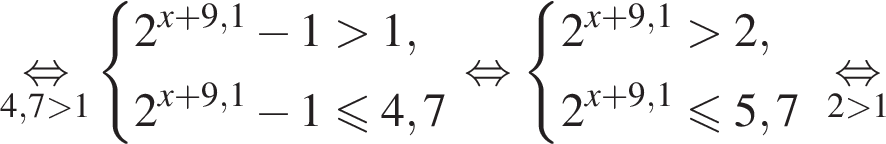
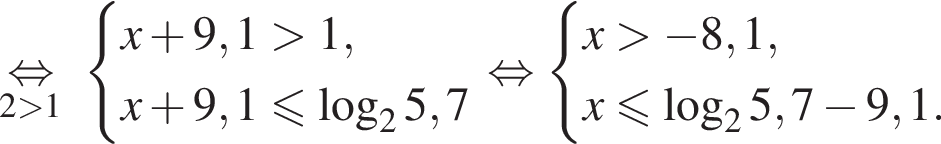
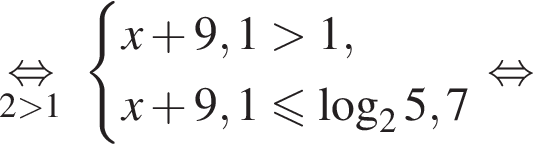
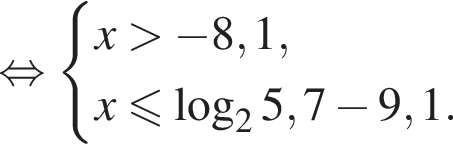
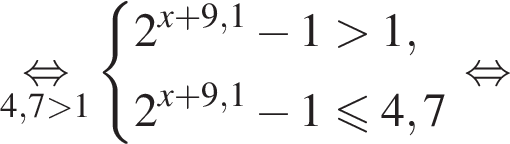
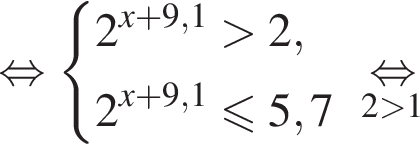
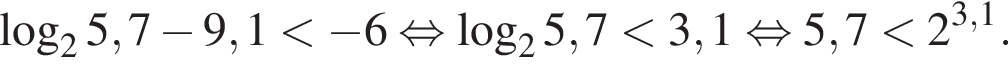
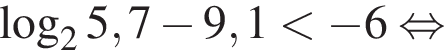
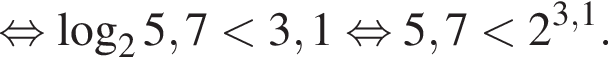
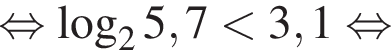

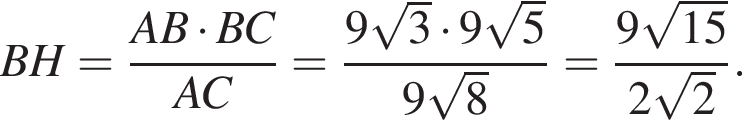
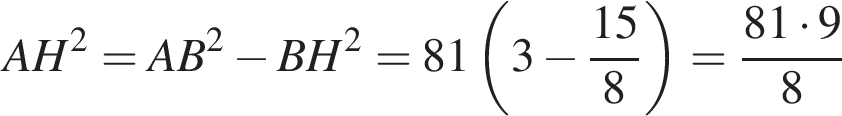
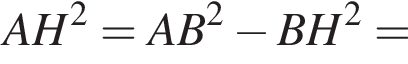
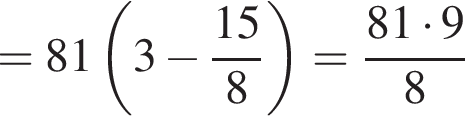
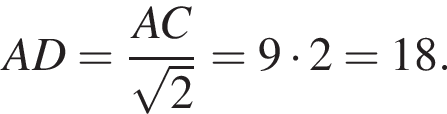
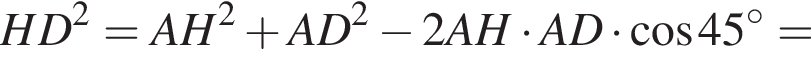
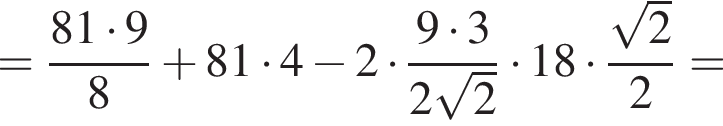
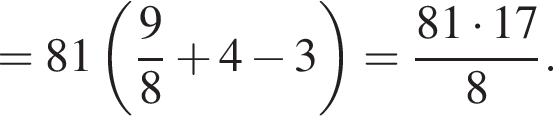


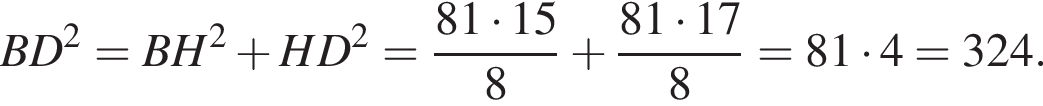

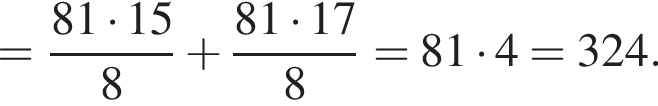
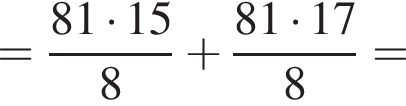
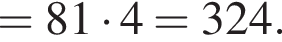

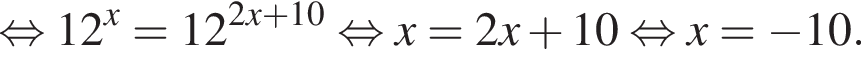
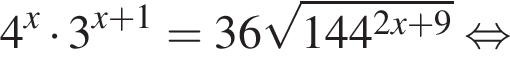
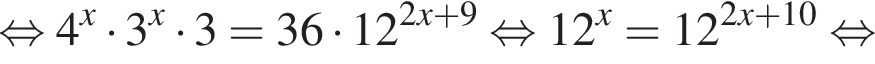
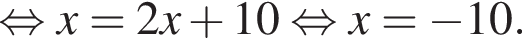
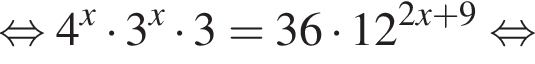
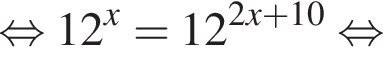
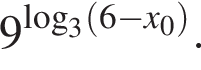 Получаем:
Получаем: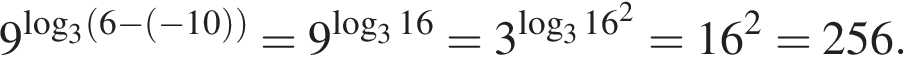
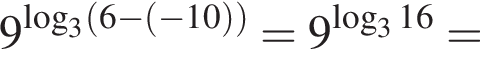
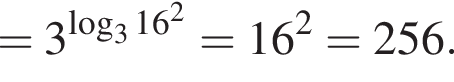
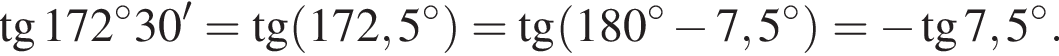
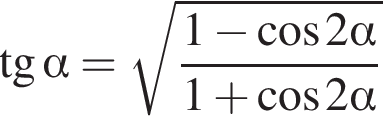 :
: 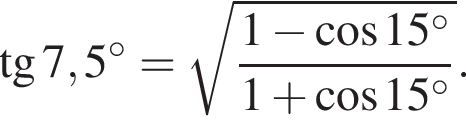



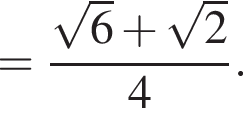
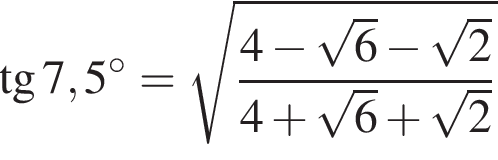
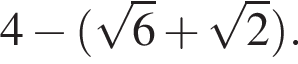 Тогда:
Тогда: 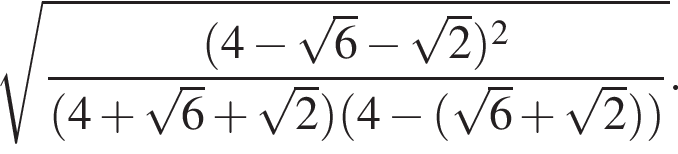
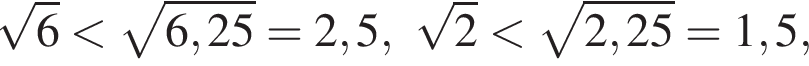
 тогда
тогда 
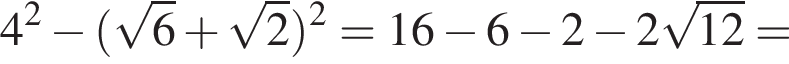

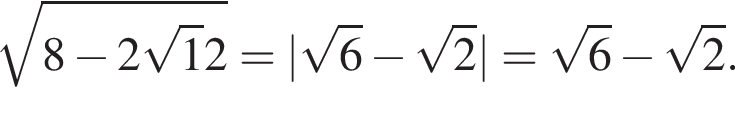 Тогда:
Тогда: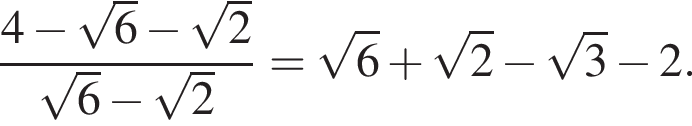
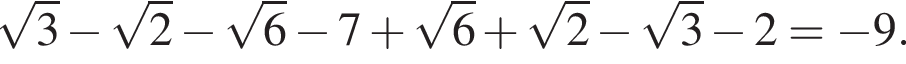

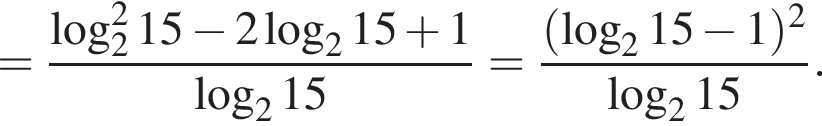
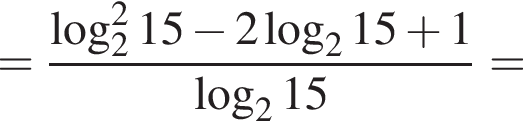
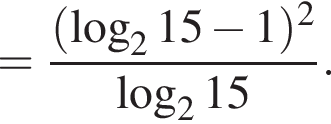
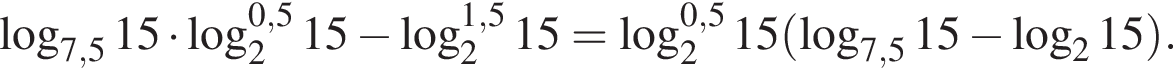
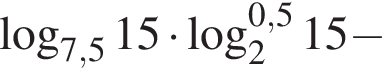
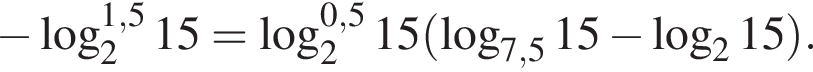
 Тогда имеем:
Тогда имеем: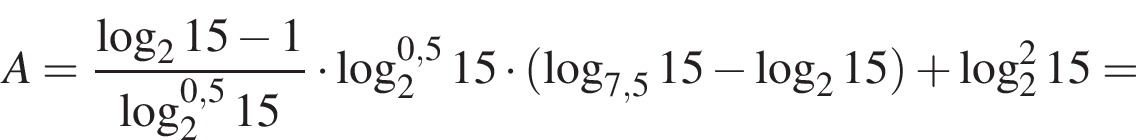
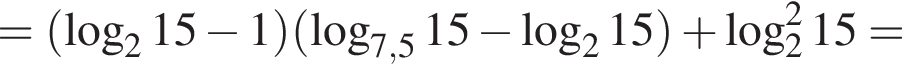
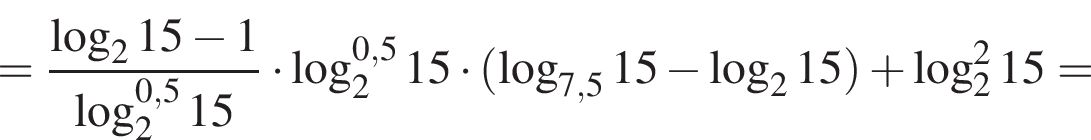
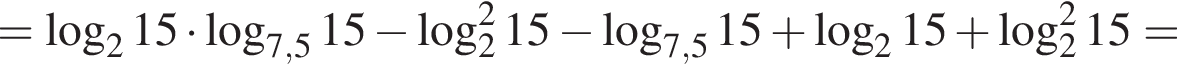
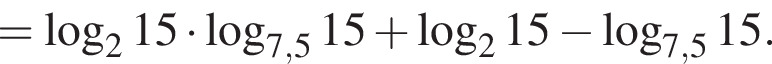
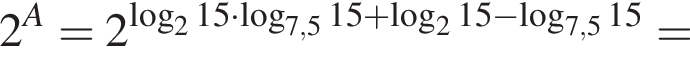
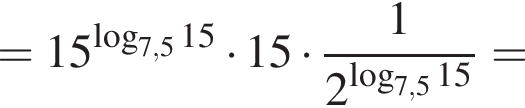
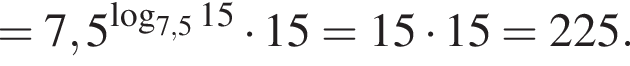
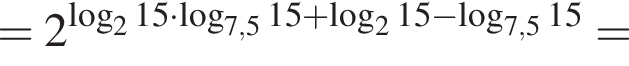
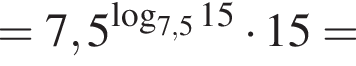
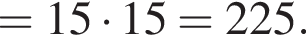
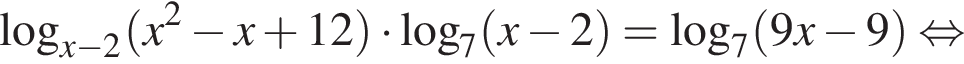
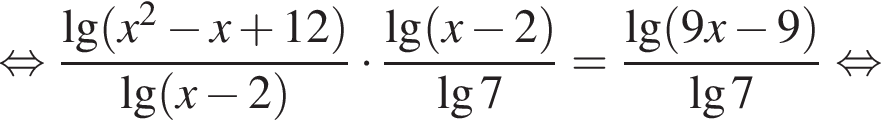
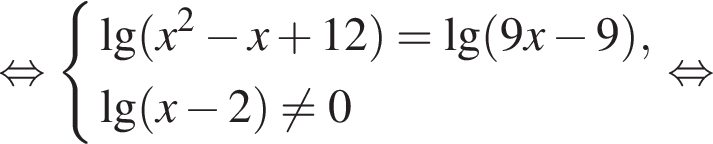
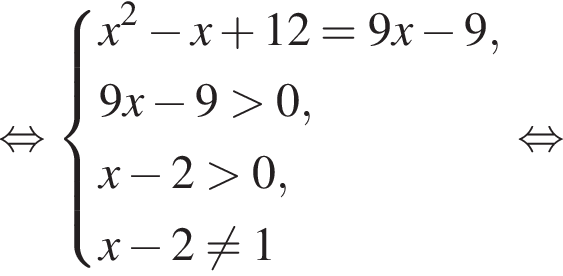
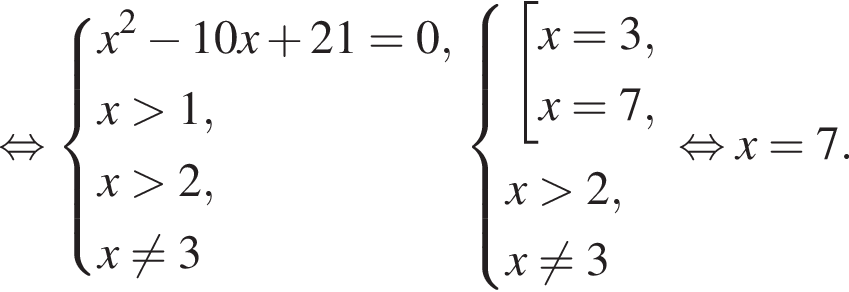
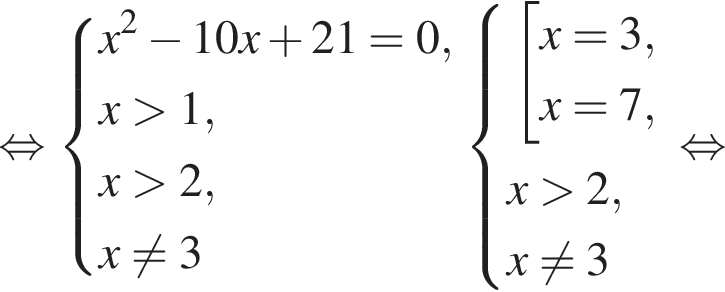

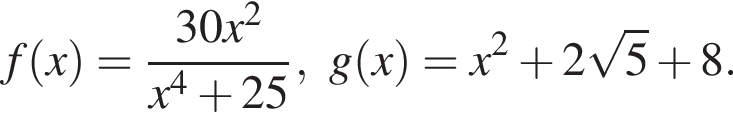
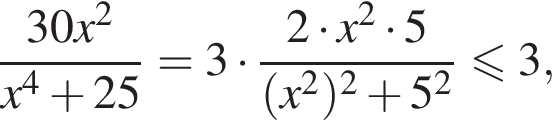 равенство достигается при
равенство достигается при 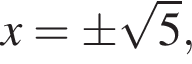 тогда
тогда 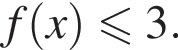
 равенство достигается при
равенство достигается при 
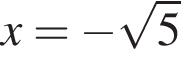 — единственный корень уравнения, тогда:
— единственный корень уравнения, тогда: 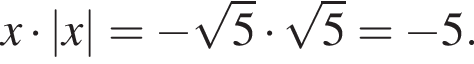
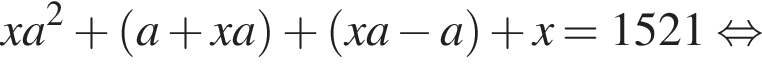
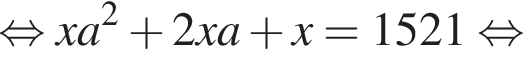

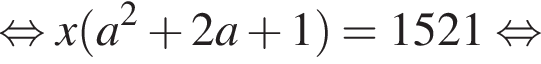
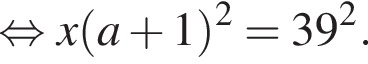
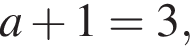
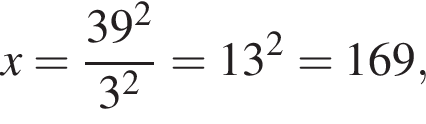
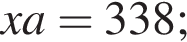
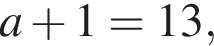
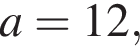
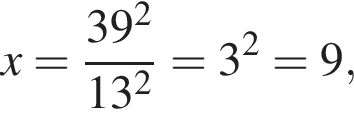
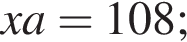
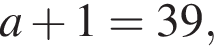
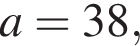
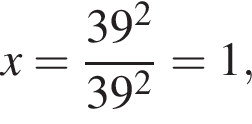
 что запрещено по условию.
что запрещено по условию.